Preliminary results

We performed a set of experiments and we presented them into the “Star Clusters and Black Holes in Galaxies Across Cosmic Time” (IAU Symposium #312) under the title GraviDy, a modular, GPU-based, direct-summation N-BODY integrator, C. Maureira-Fredes & P. Amaro-Seoane.

Experiments setup

The computational environment used for the following experiments was:

  • CPU, Intel(R) Xeon(R) CPU X5650 @ 2.67GHz (24 cores)
  • GPU, Tesla M2050 @ 575 Mhz (448 cores).
  • RAM, 24 GB
  • OS, Scientific Linux release 6.4

Results

Globular cluster evolution

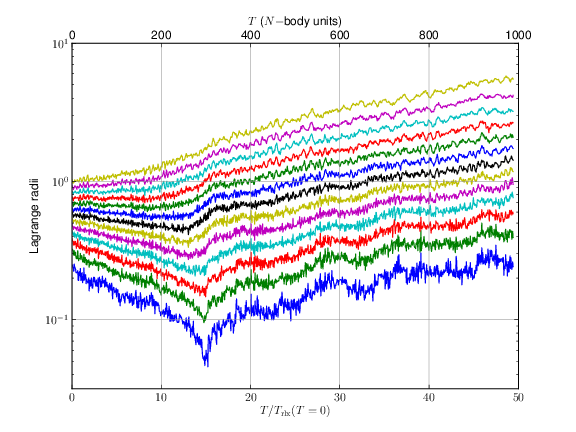
Lagrange radii of an N- body system with 1024 particles, the lines in the plot shows the radii distribution, using 5%, 10%, 15%, ..., 65% of the total mass. The core collapse is reached at \(T_{\rm cc}\,\approx\,15\,T{\rm rh}_{t=0}\), with a initial half-mass relaxation time of \(T{\rm rh}_{t=0}\,=\,20.24\) NBU.

Lagrange radii of an `N-`body system with 1024 particles.

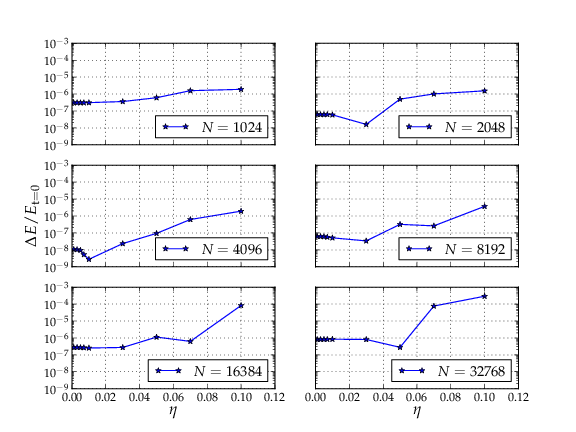
Cumulative energy error up to \(t=1\) NBU as a function of \(\eta\). All the plots represent Plummer spheres with different amount of particles (N).

Energy conservation using different values for `eta`

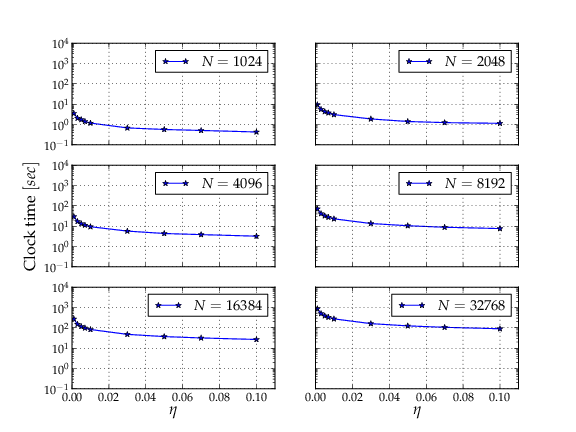
Clock time up to \(t=1\) NBU as a function of \(\eta\). All the plots represent Plummer spheres with different amount of particles (N).

Clock time as a function of `eta`

Performance

Clock time of integration from \(t=1\) to \(t = 2\) NBU using \(\eta = 0.01\) and \(\epsilon = 0.0001\) using different amount of particles (N).

Clock time as a function of `N`

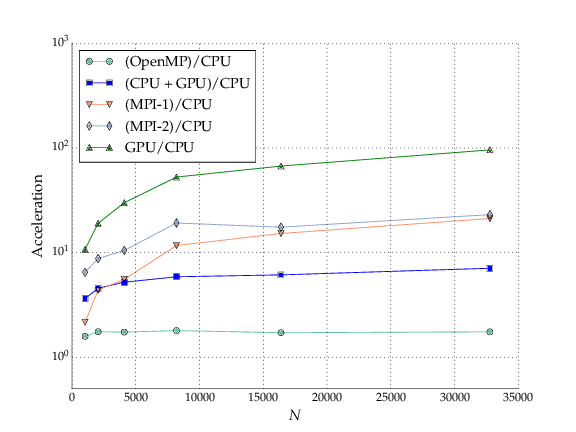
The following plot shows the acceleration of five different implementations using parallel computing techniques, compared to the single-thread base run.

  • OpenMP, ...
  • CPU + GPU, ...
  • MPI-1, ...
  • MPI-2, ...
  • GPU, ...
Speed-up

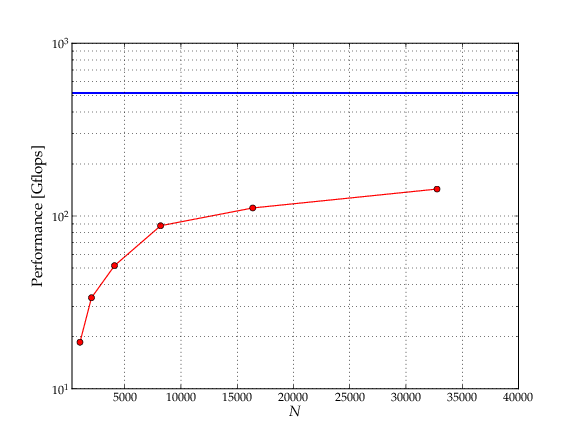
GPU gravitational interactions performance in GFLOPS for different amount of particles. The blue line at the top corresponds to the theoretical peak of the double precision floating point performance.

GFLOPs